
|
Структуры данных для представления графов Матрица примыканий обеспечивает быстрый доступ к информации о ребрах графа, однако если в графе мало ребер, то эта матрица будет содержать гораздо больше пустых клеток, чем заполненных. Длина списка примыканий пропорциональна числу ребер в графе, однако при пользовании списком время получения информации о ребре увеличивается. Ни один из этих методов не превосходит другой заведомо. В основе выбора подходящего метода должны лежать наши предварительные знания о графах, которые будут обрабатываться алгоритмом. Если в графе много вершин, причем каждая из них связана лишь с небольшим количеством других вершин, список примыканий оказывается выгоднее, поскольку он занимает меньше места, а длина просматриваемых списков ребер невелика. Если же число вершин в графе мало, то лучше пользоваться матрицей примыканий: она будет небольшой, и даже потери при хранении в матричном виде разреженного графа будут незначительны. Если же в графе много ребер и он почти полный, то матрица примыканий всегда является лучшим способом хранения графа. Использование матрицы и списка примыканий подробно описано ниже. Матрица примыканий Матрица примыканий AdjMat графа G = (V, E) с числом вершин |V| = N записывается в виде двумерного массива размером N x N. В каждой ячейке [i, j] этого массива записано значение 0 за исключением лишь тех случаев, когда из вершины vi в вершину vj ведет ребро, и тогда в ячейке записано значение 1. Говоря более строго, 
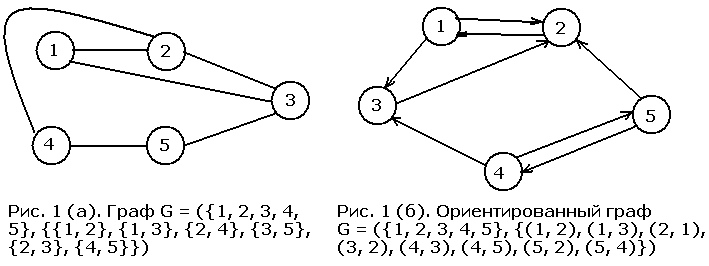

Ячейка матрицы примыканий взвешенного графа или орграфа содержит знак бесконечности, если соответствующее ребро отсутствует, а во всех остальных случаях ее значение равно весу ребра. Диагональные элементы такой матрицы равны 0, поскольку путешествие из вершины в нее саму не стоит ничего. Список примыканий Список примыканий AdjList графа G = (V, E) с числом вершин |V| = N записывается в виде одномерного массива длины N, каждый элемент которого представляет собой ссылку на список. Такой список приписан каждой вершине графа, и он содержит по одному элементу на каждую вершину графа, соседнюю с данной. На рис. 3 изображены списки примыканий для графа и орграфа, изображенных на рис. 1. Элементы списка примыканий для взвешенного графа содержат дополнительное поле, предназначенное для хранения веса ребра. 

|