
|
Основные понятия теории графов После освоения математических аспектов графов мы займемся вопросами их представления в памяти компьютера и алгоритмами их обработки. Мы увидим, что имеется много способов хранения графов, отличающихся по величине накладных расходов; выбор способа может зависеть от самого графа. Иногда приходится распространять ту или иную информацию среди большой группы людей или по всем компьютерам большой сети. Мы хотели бы, чтобы информация достигла каждого участника группы, но при этом ровно по одному разу. В некоторых группах для этой цели организуется "телефонное дерево", когда каждый из членов группы, получив свежую новость, сообщает ее небольшому числу других участников. Если каждый из членов группы встречается в дереве лишь однажды, а высота дерева не очень велика, то информация очень быстро доходит до всех. Для графов общего вида ситуация оказывается сложнее: в среднем графе гораздо больше связей, чем в дереве. Мы изучим два метода обхода графов: в глубину и по уровням, позволяющих преодолеть эту трудность. Остовное дерево представляет собой связное подмножество графа, не содержащее циклов, включающее в себя все вершины графа и некоторые из его ребер. Минимальное остовное дерево это остовное дерево, имеющее минимально возможную сумму весов ребер. Одно из применений минимальных остовных деревьев - организация внутренней компьютерной сети. Передающие станции устанавливаются в стратегически важных местах некоторой области. Если мы хотим уменьшить суммарную стоимость объединения станций в сеть, то можно нарисовать граф, в котором станции будут служить вершинами, а ребрам, их соединяющим, можно приписать стоимость соединения. Минимальное остовное дерево этого графа указывает, какие станции следует соединить между собой, чтобы любые две станции оказались соединенными, причем общая стоимость соединения была минимально возможной. Аналогичные приложения имеет и задача поиска кратчайшего пути в графе: умение решать такую задачу помогает планировать путь на автомобиле или посылать сообщение по компьютерной сети. Важной характеристикой большой компьютерной сети служит ее надежность. Мы хотели бы, чтобы сеть сохраняла работоспособность при выходе из строя одного узла. Говоря проще, станции в сети должны быть соединены несколькими путями, чтобы при разрушении какого-либо из путей возможность передачи информации сохранялась. В последнем параграфе этой главы мы обсуждаем алгоритм поиска компонент двусвязности. Он ищет вершины, неизбежно находящиеся на всяком пути из одной части графа в другую. В компьютерной сети разрушение таких узлов приводит к нарушению связности сети. С формальной точки зрения граф представляет собой упорядоченную пару G = (V, Е) множеств, первое из которых состоит из вершин, или узлов, графа, а второе - из его ребер. Ребро связывает между собой две вершины. При работе с графами нас часто интересует, как проложить путь из ребер от одной вершины графа к другой. Поэтому мы будем говорить о движении по ребру; это означает, что мы переходим из вершины А графа в другую вершину В, связанную с ней ребром АВ (ребро графа, связывающее две вершины, для краткости обозначается этой парой вершин). В этом случае мы говорим, что А примыкает к В, или что эти две вершины соседние. Граф может быть ориентированным или нет. Ребра неориентированного графа, чаще всего называемого просто графом, можно проходить в обоих направлениях. В этом случае ребро - это неупорядоченная пара вершин, его концов. В ориентированном графе, или орграфе, ребра представляют собой упорядоченные пары вершин: первая вершина - это начало ребра, а вторая - его конец. Далее мы для краткости будем говорить просто о ребрах, а ориентированы они или нет будет понятно из контекста. Позже мы будем просто рисовать графы, а не задавать их множествами. Вершины будут изображаться кружочками, а ребра - отрезками линий. Внутри кружочков будут записаны метки вершин. Ребра ориентированного графа будут снабжены стрелками, указывающими допустимое направление движения по ребру. На рисунке 1 изображено графическое представление неориентированного (а) и ориентированного (б) графов вместе с их формальным описанием. 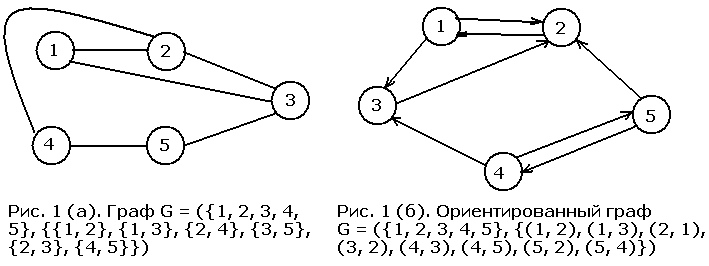
Терминология Полный граф - это граф, в котором каждая вершина соединена со всеми остальными. Числ ребер в полном графе без петель с N вершинами равно (N2 - N)/2. В полном ориентирвоанном графе разрешается переход из любой вершины в любую другую. Поскольку в графе переход по ребру разрешается в обоих направлениях, а переход по ребру в орграфе - только в одном, в полном орграфе в два раза больше ребер, то есть их число равно N2 - N. Подграф (VS, ES) графа или орграфа (V, E) состоит из некоторого подмножества вершин и некоторого подмножества ребер, их соединяющих. Путь в графе или орграфе - это последовательность ребер, по которым можно поочередно проходить. Другими словами, путь из вершины A в вершину B начинается в A и проходит по набору ребер до тех пор, пока не будет достигнута вершина B. С формальной точки зрения, путь из вершины vi в вершину vj это последовательность ребер графа vivi+1, vi+1vi+2, ..., vj-1vj. Мы требуем, чтобы любая вершина встречалась на таком пути не более, чем однажды. У всякого пути есть длина - число ребер в нем. Длина пути AB, BC, CD, DE равна 4. Во взвешенном графе или орграфе каждому ребру приписано число, называемое весом ребра. При изображении графа обычно записывают вес ребра рядом с ребром. При формальном описании вес будет дополнительным элементом неупорядоченной или упорядоченной пары вершин (образуя вместе с этой парой "триплет"). При работе с ориентированными графами мы считаем вес ребра ценой прохода по нему. Стоимость пути по взвешенному графу равна сумме весов ребер пути. Кратчайший путь во взвешенном графе - это путь с минимальным весом, даже если число ребер в пути и можно уменьшить. Если, например, путь P1 состоит из пяти ребер с общим весом 24, а путь P2 - из трех ребер с общим весом 36, то путь P1 считается более коротким. Граф или орграф называется связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл - это путь, который начинается и кончается в одной и той же вершине. В ациклическом графе или орграфе циклы отсутствуют. Связный ациклический граф называется (неукорененным) деревом. Структура неукорененного дерева такая же, что и у дерева, только в нем не выделен корень. Однако каждая вершина неукорененного дерева может служить его корнем. |