При работе с графами часто приходится выполнять некоторое действие по одному разу с каждой из вершин графа. Например, некоторую порцию информации следует передать каждому из компьютеров в сети. При этом мы не хотим посещать какой-либо компьютер дважды. Аналогичная ситуация возникает, если мы хотим собрать информацию, а не распространить ее.
     Подобный обход можно совершать двумя различными способами. При обходе в глубину проход по выбранному пути осуществляется настолько глубоко, насколько это возможно, а при обходе по уровням мы равномерно двигаемся вдоль всех возможных направлений. Изучим теперь эти два способа более подробно. В обоих случаях мы выбираем одну из вершин графа в качестве отправной точки. Ниже под "посещением узла" мы понимаем выполнение действия, которое необходимо совершить в каждой вершине. Если, например, идет поиск, то фраза о том, что мы посетили данный узел, означает, что мы проверили его на наличие требуемой информации. Описываемые методы работают без каких-либо изменений как на ориентированных, так и на неориентированных графах. Мы будем иллюстрировать их на неориентированных графах.
     С помощью любого из этих методов можно проверить, связен ли рассматриваемый граф. При обходе графа можно составить список пройденных узлов, а по завершении обхода составленный список можно сравнить со списком всех узлов графа. Если списки содержат одни и те же элементы, то граф связен. В противном случае в графе есть вершины, до которых нельзя дойти из начальной вершины, поэтому он несвязен.

Обход в глубину
     При обходе в глубину мы посещаем первый узел, а затем идем вдоль ребер графа, пока не упремся в тупик. Узел неориентированного графа является тупиком, если мы уже посетили все примыкающие к нему узлы. В ориентированном графе тупиком также оказывается узел, из которого нет выходящих ребер.
     После попадания в тупик мы возвращаемся назад вдоль пройденного пути пока не обнаружим вершину, у которой есть еще не посещенный сосед, а затем двигаемся в этом новом направлении. Процесс оказывается завершенным, когда мы вернулись в отправную точку, а все примыкающие к ней вершины уже оказались посещенными.
     Иллюстрируя этот и другие алгоритмы обхода, при выборе одной из двух вершин мы всегда будем выбирать вершину с меньшей (в числовом или лексикографическом порядке) меткой. При реализации алгоритма выбор будет определяться способом хранения ребер графа.
     Рассмотрим граф с рис. 1. Начав обход в глубину в вершине 1, мы затем посетим последовательно вершины 2, 3, 4, 7, 5 и 6 и упремся в тупик. Затем нам придется вернуться в вершину 7 и обнаружить, что вершина 8 осталась непосещенной. Однако, перейдя в эту вершину, мы немедленно вновь оказываемся в тупике. Вернувшись в вершину 4, мы обнаруживаем, что непосещенной осталась вершина 9; ее посещение вновь заводит нас в тупик. Мы снова возвращаемся назад в исходную вершину, и поскольку все соседние с ней вершины оказались посещенными, обход закончен.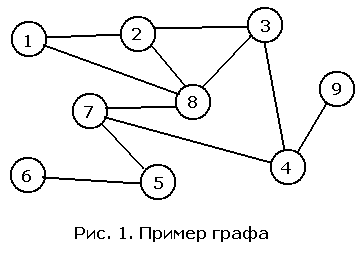

     Вот как выглядит рекурсивный алгоритм обхода в глубину:

DepthFirstTraversal (G, v)
G	граф
v	текущий узел
Visit(v)
Mark(v)
for каждого ребра vw графа G do
	if вершина w непомечена then
		DepthFirstTraversal(G, w)
	end if
end for
			

BreadthFirstTraversal(G, v)
G	граф
v	текущий узел
Visit(v)
Mark(v)
Enqueue(v)
while очередь непуста do
	Dequeue(x)
	for каждого ребра xw в графе G do
		if вершина w непомечена then
			Visit(w)
			Mark(w)
			Enqueue(w)
		end if
	end for
end while